hypesoli.blogg.se - Trapezoid base one 10cm base two 5cm height 2cm equals

#TRAPEZOID BASE ONE 10CM BASE TWO 5CM HEIGHT 2CM EQUALS HOW TO#

area A of a triangle equals one half the product of the length of a base and the height. In the next section, we will discuss different types of a trapezoid. Geometry Figure 3 below shows two lines, l sub 1 and l sub 2. The following equation will be true for this trapezoid:

Suppose there is a trapezoid with sides a, b, c, and d and its diagonals are p and q.

The point of concurrency of the diagonals of the trapezoid is collinear to the midpoints of two opposite sides.

The median of the trapezoid will be parallel to the bases and its length will be equal to the average of the length of its bases. Before we can use the area formula, we first have to determine the height of the trapezoid.

The diagonals and base angles of an isosceles trapezoid are equal.

Some of the important properties of the trapezoid are given below: Like other geometrical figures, trapezoids have their unique properties that set them apart from other figures. Finally, apply the formula for the area of a trapezoid: A (a + b) × h / 2 (4 + 1.675) × 6 / 2 17.026 cm. In the next section, we will discuss certain properties of the trapezoid. Subtract the values of a, c, and d from the trapezoid perimeter to find the length of the second base: b P - a - c - d 25 - 4 - 12 - 7.325 1.675 cm. A quadrilateral is a figure having four sides. 10 cm edges and the base of the prism is a 5 cm by 10 cm rectangle, find the height h of the. Hence, we can say that a trapezoid is a type of quadrilateral. However, the first school of thought does not consider a parallelogram a trapezoid. If the argument of the second school is accepted then we can say that a parallelogram is also a trapezoid because it has more than one pair of parallel sides. On the other hand, the other school argues that a trapezoid can have more than one pair of parallel sides. One school says that a trapezoid has only one pair of parallel sides. There are two schools of thought on the definition of the trapezoid or trapezium. The height of O A B can be found in various ways.

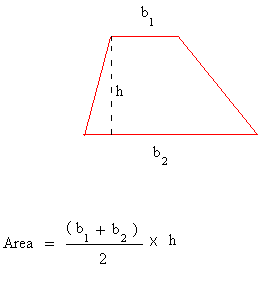
That is 1 + 7 20 times the height of O A B. If we want to use the usual formula for the area of a trapezoid, all we need is the height of the trapezoid. The shape of the trapezoid resembles that of a square, rectangle, and parallelogram. A O ( 20) ( 13) 27, and similarly, B O ( 20) ( 5 10) 27. An altitude of a trapezoid refers to the distance between two parallel sides.

On the other hand, the legs or lateral sides of the trapezoids are those sides that are non-parallel. The bases of trapezoids are the sides that are parallel to each other. These two-dimensional figures cover some areas and have their perimeters. Trapezoids, also known as a trapezium, are four-sided geometrical figures. Example 2: Find the area of a triangle whose sides and the angle between them are given as following: a 5cm and b 7cm C 45 o. The quadrilateral having two parallel sides is known as a trapezoid Example 1: Find the area of a triangle whose base is 14 cm and height is 10 cm.

We take half the sum of the length of the two bases (their average) and. Multiplying times 1 2 1 2 is the same as dividing by 2. In the formula, the long and short bases are a a and b b, and the altitude is h h: area a+b 2 h a r e a a + b 2 h. Before discussing the types and properties of trapezoids, first, let us define a trapezoid. The area of parallelogram with base 2.5 cm height 3 cm equals to triangle its side length 5 cm Find the height of triangle. The formula for the area of a trapezoid is the average of the bases multiplied by the altitude.

#TRAPEZOID BASE ONE 10CM BASE TWO 5CM HEIGHT 2CM EQUALS HOW TO#

Therefore, the pressure here will be #P=(37.5 \ "N")/(0.03 \ "m"^2)=1250 \ "Pa"#.In this article, we will discuss what are trapezoids, their properties, different types, and how to calculate their area and perimeter. If we want to apply the least possible pressure, we must apply the force on the face with the biggest dimensions, and that is #0.3 \ "m"# by #0.1 \ "m"#, and #A=0.3 \ "m"*0.1 \ "m"=0.03 \ "m"^2#. So, we would want to apply the force on the face of the block with the smallest dimensions if we want to find the largest pressure, i.e. bigger area equals less pressure, smaller area equals bigger pressure. Therefore, pressure is inversely proportional to area, i.e. Since the force is constant, we can let #F=k#, and we have So, we got the rectangular block with dimensions #30 \ "cm"# by #5 \ "cm"# by #10 \ "cm"#, or if we write this in meters, it is #0.3 \ "m"# by #0.05 \ "m"# by #0.1 \ "m"#. Where #F# is the force in newtons, and #A# is the area in #"m"^2#. Pressure is defined through the equation: